卡尔曼滤波，好像理解了

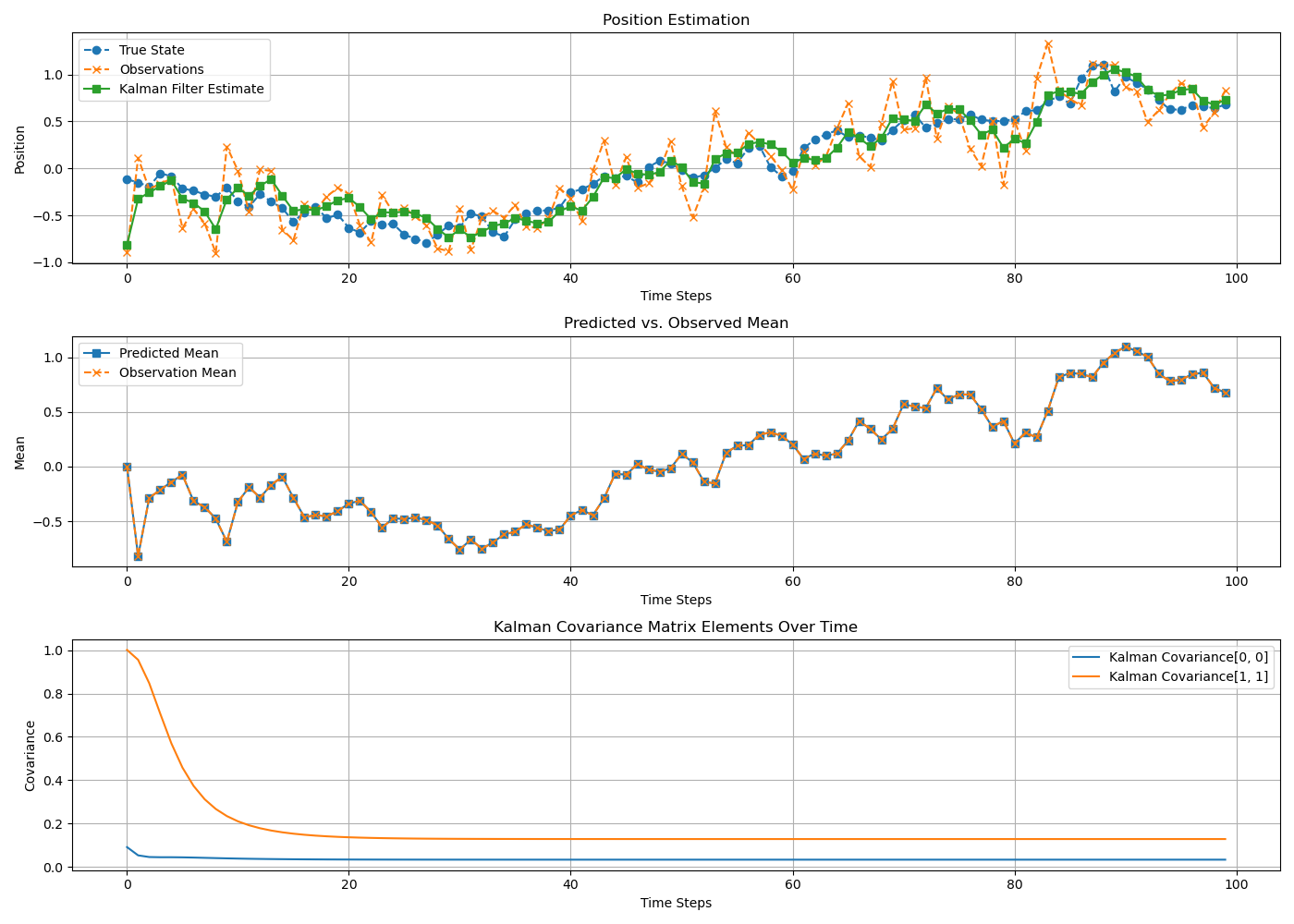
参考：https://www.guyuehome.com/33293
部分附图来源： https://zhuanlan.zhihu.com/p/39912633 如有侵权，联系删除

部分公式使用了国外API进行解析，可能加载不出来，需要科学上网

！！！个人对卡尔曼整个过程的思路理解

总结在前（包含其他网上的理解）

卡尔曼滤波实质就是将预测状态量的高斯分布和观测量的高斯分布做融合，生成一个新的高斯分布，其中新的高斯分布的均值和方差是两个独立的高斯分布的相关参量的加权，这个加权就是卡尔曼增益，但是预测状态量和观测量可能维度不同，需要将他们同时转换到一个向量空间中，所以观测量前面有线性变换矩阵
记得有教科书写过，估计过去的状态叫平滑，估计当前的状态叫滤波，估计未来的状态叫预测
只从最后公式的角度看，确实是加权平均，我一开始也是这样理解的，所以特别想分享一下我现在的理解。在看过英语版原文之后，我发现这篇文章的翻译水准实在不敢恭维，译者似乎并没有本质上理解kalman滤波是在干什么。本质上，kalman滤波做了2件事:
\1. 基于前一时间点的系统状态的概率分布给出当前时间点的系统状态的概率分布预测P1
\2. 基于当前时间点的观测量的概率分布Q给出另一组对当前时间点系统状态的概率分布预测P2 (这里需要注意，如果传感器能直接把系统状态都观测了，那么我们直接用观测量的概率分布Q作为P2就好了，但是有可能传感器观测的物理量量并不是直接的系统状态，而是其他物理量，这时我们需要通过做一个线性变换来获得P2)

现在，我们有两个关于当前时间点系统状态的概率分布的预测P1和P2，我们于是可以计算它们的联合概率分布，也就是为什么文章中要把两个概率分布乘到一起去。这个联合概率分布就是我们最终想要的更正过后的当前时间点的系统状态概率分布，有了它我们就可以进入下一个时间点继续迭代我们交替的预测-更正步骤了

预测过程

物体的状态 X (x1,x2,x3,....xn)

状态量 xi 之间可能存在某种关系（可能难以用数学公式描述，但我们知道是存在的）

如速度v 和位置p

速度v 大的话，我的位置p 变换也就大

速度v 小的话，位置 p 变化也就小

但我们可以描述状态量 i 之间的相关性用协方差矩阵 $\sum_{n \times n}$ ，称为 P_k

状态 X 的转换可以用转换矩阵 F_k ，来表示我们的预测步骤

例如

$\begin{bmatrix}p_t\\v_t\end{bmatrix}=\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}\begin{bmatrix}p_{t-1}\\v_{t-1}\end{bmatrix}$

这样的 F_k 是基于一些自然定律，来完成状态更新，

但同时可能外界的一些因素也会影响状态的更新【比如，运动中突然的加速指令减速指令】

将这些因素（也就是我们对状态定义中不关心的因素，但是影响状态）称为 u_k 外部输入或控制输入

其中这些外部输入也会以某种规则来影响状态，我们将这种定义的规则，以矩阵的形式表示B_k，称为输入矩阵或控制矩阵

例如

$\hat{X}_k=F_k\hat{X}_{k-1}+B_k\vec{u}_k$

但这样，还是会有一些因素我们无法考虑进去，比如说，今天的温度，这些我们称之为噪声或过程噪声，然后我们把这个同样形式化为矩阵 W_k

$\hat{X_k}=F_k\hat{X}_{k-1}+B_k\vec{u}_k+W_k$

这样，我们的整个状态方程就出来了，

!!! 一般情况下，我们不考虑这种过程噪声，甚至当我们的环境非常简单，后面的输入变量和输入矩阵也可以忽略

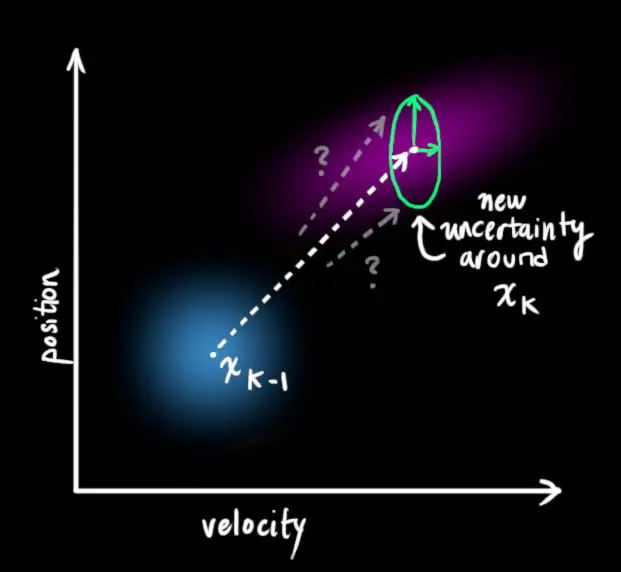
由于这些种种因素【不确定性】，我们的状态就很难准确表示出来，这时，我们想到的是用概率分布进行建模

状态是处于一个概率分布上的，一个状态有多个状态量，每一个状态量我们都用概率分布进行建模

我们最常用的概率分布就是高斯分布（也叫标准正态分布）

在上面，我们提到了状态量之间是存在相关性的，我们用协方差矩阵表示

但这个协方差矩阵只能描述状态量之间的相关性，如何去刻画这些其他外部因素的造成的不确定性，具体的做法，我们是在预测上添加 "不确定性" Q_k 【将这些不确定性影响视为了协方差 Q_k 的噪声】

我们的协方差矩阵更新，也就得到了

$\hat{P_k}=F_k\hat{P}_{k-1}F_k^{T}+Q_k$

另一个角度理解：

由于不确定性，状态的分布范围变大了【也就是状态的位置不同】，这个分布范围的状态均值一定，我们想要将这些分布范围联系起来，【不同位置的状态仍然是高斯分布，我们将不同位置联系起来，也就是将高斯分布联系起来】这样会产生一个新的高斯分布，协方差不同，均值相同

所以，我们在这里添加的Q_k 就是针对那些不确定性进行建模

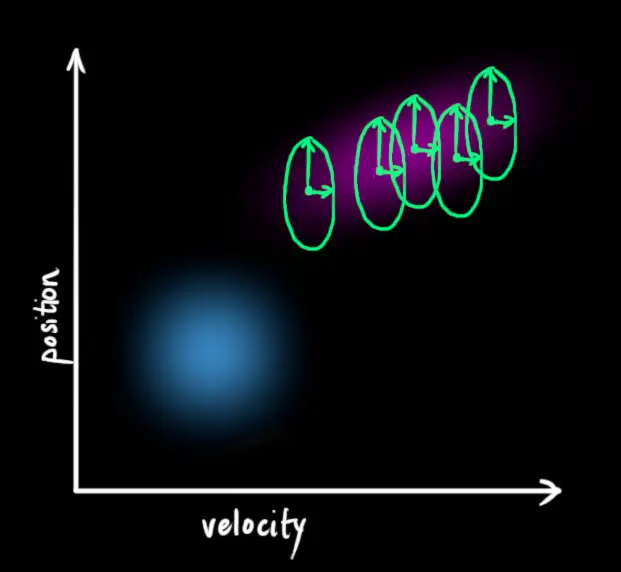
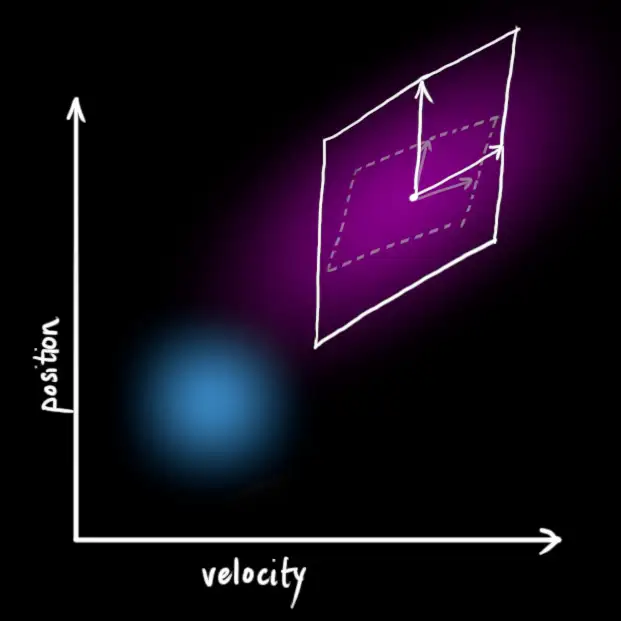
这样的两个公式我们称之为预测状态方程和预测协方差方程

$\hat{X_k}=F_k\hat{X}_{k-1}+B_k\vec{u}_k+W_k$

$\hat{P_k}=F_k\hat{P}_{k-1}F_k^{T}+Q_k$

这个过程也称为预测过程

通过这个预测过程我们得到了，预测的状态估计X_k，预测协方差矩阵 P_k

观测过程（这里理解的不是很好）

预测后我们需要对状态进行更新

但同时我们可以得到一些观测信息，

我们状态转移的分布和观测值的单位可能不同【或者说是所处空间不同，我们使用矩阵 H_k 对状态转移分布进行转换】

$$
\mu = H_k \hat{x}_k \\ \sum = H_k P_k H_k^T
$$
我们期望观测值也可以被建模成这样

同时观测值本身也存在噪声、不确定性等因素

观测方程
$$
z_k = H_k X_k + u_k
$$
其中，z_k 是观测值，H_k 是观测矩阵，u_k 是观测噪声。

观测分布的均值表示在考虑观测信息后，系统状态的预测值在观测空间中的投影。

这样，我们将观测值的协方差表示为 R_k，均值表示为 z_k

均值通过观测方程计算
$$
\hat{z}_k = H \hat{x}_k'
$$
其中

$\hat{x}_k'$ 是预测步骤得到的预测状态值
H 是观测矩阵

协方差计算如下：
$$
S_k = H \hat{P}_k H^T+R
$$
其中

$\hat{P}_k$ 是预测步骤得到的协方差矩阵
R 为观测噪声的协方差矩阵

以上的计算都发生在完成预测过程完成后，但分布信息并不参与下面的更新过程

在下面的更新中，我们使用的是当前观测信息 z_k，R，而不是观测分布均值（\hat{z}_k S_k）

这样我们其实得到了两个高斯分布

预测状态转移的高斯分布

$(\mu_{0},\Sigma_{0})=(\mathrm{H}_{k}\hat{\mathbf{x}}_{k}, \mathrm{H}_{k}\mathrm{P}_{k}\mathrm{H}_{k}^{T})$

当前观测信息的高斯分布（）

$(\mu_{1},\Sigma_{1})=({z}_k,\mathrm{R}_{k})$

我们将这两个高斯分布进行融合【也就是高斯分布进行相乘，得到一个新的高斯分布】，得到最终的最优分布

高斯分布处理

两个高斯分布相乘
$$
N(x,\mu,\sigma) = \frac 1 {\sigma \sqrt{2 \pi}} e^{ - \frac {(x-\mu)^2}{2 \sigma^2}}
$$

$$
N(x,\mu_0,\sigma_0) N(x,\mu_1,\sigma_1) = N(x,\mu',\sigma')
$$

$\mu'=\mu_0 + \frac {\sigma_0^2(\mu_1 - \mu_0)}{\sigma_0^2 + \sigma_1^2} \\ \sigma'^2 = \sigma_0^2 - \frac {\sigma_0^4 }{\sigma_0^2 + \sigma_1^2}$

将其中一部分重写为 k

$\mathbf{k}=\frac{\sigma_{0}^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}}$

然后公式就可以重写为

$\begin{array}{c}{{\mu^{\prime}=\mu_{0}+{\bf k}(\mu_{1}-\mu_{0})}}\\\\ {{\sigma^{\prime}=\sigma_{0}^{2}-{\bf k}\sigma_{0}^{2}}}\end{array}$

然后矩阵形式

$\mathbf{K}=\Sigma_{0}(\Sigma_{0}+\Sigma_{1})^{-1}\\\\ \begin{array}{l c r}{{\vec{\mu}^{\prime}=\vec{\mu}_{0}+{\bf K}(\vec{\mu}_{1}-\vec{\mu}_{0})}}\\\\ {{\sum^{\prime}=\sum_{0}-{\bf K}\Sigma_{0}}}\end{array}$

$\sum'$ 表示新高斯分布的协方差矩阵，$\mu$ 是每一个维度（状态量）的矩阵

K 就是

$\mathbf{K}=\Sigma_{0}(\Sigma_{0}+\Sigma_{1})^{-1}$

卡尔曼增益 kalman gain

更新过程

然后我们通过这两个分布进行状态更新

预测状态转移的高斯分布

$(\mu_{0},\Sigma_{0})=(\mathrm{H}_{k}\hat{\bf x}_{k},\mathrm{H}_{k}\mathrm{P}_{k}\mathrm{H}_{k}^{T})$
观测信息的高斯分布

$(\mu_{1},\Sigma_{1})=(\hat{z}_k,\mathrm{R}_{k})$

这样我们就可以得到更新的状态

然后对应的各状态量利用这个最终的分布进行更新

$\begin{array}{l c r}{{\vec{\mu}^{\prime}=\vec{\mu}_{0}+{\bf K}(\vec{\mu}_{1}-\vec{\mu}_{0})}}\\ {{\sum^{\prime}=\sum_{0}-{\bf K}\Sigma_{0}}}\end{array}$

两个分布带入上式

$H_k \hat{X}'_k = H_k \hat{X}_k + {\bf K} (\hat{z}_k - H_k \hat{X}_k) \\ H_k P_k' H_k^T = H_k P_k H_k^T - {\bf K} H_k P_k H_k^T$

卡尔曼增益

$K = \mathrm{H}_{k}\mathrm{P}_{k}\mathrm{H}_{k}^{T}( \mathrm{H}_{k}\mathrm{P}_{k}\mathrm{H}_{k}^{T} + R_k)^{-1}$

同时上式我们可以看到包含一个 H_k，可以做进一步精简

$\begin{array}{c}{{\hat{X}_{k}'=\hat{X}_{k}+K_{k}'\cdot(\hat{z}_{k}-H_{k}\cdot\hat{X}_{k})}}{{{}}}\\{{P_{k}'=\left(I-K_{k}'\cdot H_{k}\right)\cdot P_{k}}}\end{array}$