在学习 numpy,torch 时,在很多运算中,我们都会遇到 axis or dim 这个参数
之前学习的时候,一个API 也就过去了,但有时候在一个具体的场景里,又会对这个 axis (dim) 需要进行 考虑,而不是直接调用 API扔进去就行,因此我们需要去搞明白这个 axis,dim,本文理解起来,非常友好,同时在最后也可以引起大家一些思考。
ok,让我们开始,首先直接给出观点
axis 或者 dim 是方向 !
三维
import numpy as np
# 生成数据 模仿图片 shape c w h
img = np.arange(27).reshape(3,3,3)现在我们得到了一张图片【图像是有RGB通道,所以是三维】
一些常见的运算,让我们去求最大值max,最小值 min,求和sum,均值mean, 方差var 等等
np.max()
np.min()
np.sum()
np.mean()
np.var()
# ...一般情况下,我们遇到的数据可能是一些简单的一维或者二维数据,直接丢进去,就可以获得我们需要的 全局结果【注意,我这里说的是一个全局结果】,
但在某些高维数据,或者某些场景中,我们需要的不是这种全局结果,而是某一部分的 值 ,如 一行里面的最大值,一列里面的最大值,又或者是 通道内的最大值,这些在高维数据中,我们就无法直接丢进去,而是需要去指定 axis
拿 image 为例 其shape 为 c,h,w,也即三个维度
# 这里以求和为例
np.sum(img)
np.sum(img,axis=0)
np.sum(img,axis=1)
np.sum(img,axis=2)
# 与上面效果等价
np.sum(img,axis=-3)
np.sum(img,axis=-2)
np.sum(img,axis=-1)打印输出结果

对于输出的结果,你能理解吗
记住我们的观点,axis 是方向
c,h,w 三维,我们可以将这个图像数据理解为 一个 长方体
axis = 0 即 c 维度 ,我们将其理解为 长方体的 高
axis = 1 即 h 维度,我们将其理解为 长方体的 长
axis = 1 即 w 维度,我们将其理解为 长方体的 宽
现在再来看一下
# axis =0
# 0,9,18 = 27 即取 长方体 高的方向上的 对应元素进行求和
# axis = 1
# 0,3,6 = 9
# axis = 2
# 0,1,2 = 3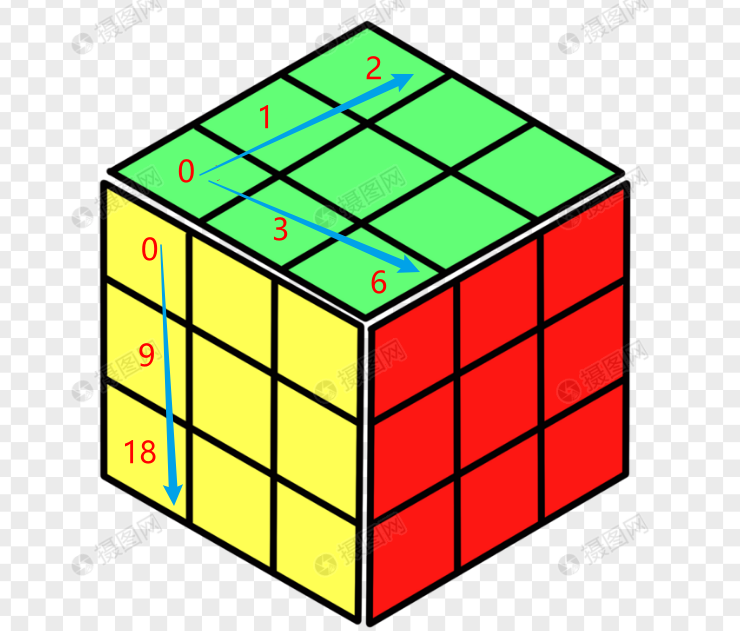
【这里找了一个魔方图,进行理解】
是不是就很容易理解了,
axis 参数还可以是 元组 ,在这里可以是 (0,1),(1,2) ,(0,2)
这样就是 同时沿着 两个方向进行计算,
这里以axis=(0,1)为例
np.sum(img,axis=(0,1))
'''
输出结果
[108 117 126]
0,9,18 , 3,12,21 6,15,24 = 108
'''现在应该理解了吧,所以 axis 是方向,
明白了这个,对于在真实的数据场景中 还是很有帮助的
四维或者更高维
之前图像是三维,那当更高维度如何理解
在神经网络中,数据的形状 常常是 B,C,H,W
这里加入了一个B维度,变成了四维,在这里,提供了一个可视化的理解,
我们可以把 B 这个维度 想象成一个 时间维度,
可以想象一下 在时间的维度上 有各种不同的 C H W 排布,那么当我们在这个四维上进行 这些运算,依然还是可以应用这种对axis的理解方法
这里进行一下模拟
img = img.reshape(1,3,3,3)
batch = np.repeat(img,2,axis=0)
# batch (2,3,3,3)
# 运算
# 这里举一个简单例子
np.sum(batch,axis=0)
'''
result
[[[ 0 2 4]
[ 6 8 10]
[12 14 16]]
[[18 20 22]
[24 26 28]
[30 32 34]]
[[36 38 40]
[42 44 46]
[48 50 52]]]
'''这个结果 你是否又理解了
按照我们的理解,axis是方向,axis=0 即是B 方向,可视化的理解就是 一种时间
那么在时间的维度上 排布着许多 CHW 这种长方体,现在我们进行求和,可以理解为把他们变成一个长方体,长方体内部对应的数字进行相加,就完成了在 B维度上的求和,也就是我们看到的这个结果 每个值变成了原来2倍。
-
目前为止的话,理解到四维,对于我们的学习应该是够了,至少是在大多数神经网络数据形式上。
-
dim 是 torch 中的说法,和numpy 中 的 axis 是一样的
-
axis 是方向 !!!
思考
更高维呢???
有没有可视化的理解呢????
欢迎大家来讨论,
